Multiplication with FPGA DSPs
Welcome back to my series covering mathematics and algorithms with FPGAs. Project F is known for its practical, hands-on tutorials. So, I decided to dedicate a post to a topic usually ignored by FPGA authors: multiplication with DSPs. New to the series? Start with Numbers in Verilog.
Series Outline
- Numbers in Verilog - introduction to numbers in Verilog
- Vectors and Arrays - working with Verilog vectors and arrays
- Multiplication with FPGA DSPs (this post) - efficient multiplication with DSPs
- Fixed-Point Numbers in Verilog - precision without complexity
- Division in Verilog - divided we stand
- More maths to follow
DSP Blocks
FPGAs incorporate dedicated digital signal processing (DSP) blocks. As their name suggests, DSPs accelerate typical signal processing tasks, such as fast Fourier transforms (FFTs) and finite impulse response filtering (FIR). DSP blocks include multipliers, which we’ll cover in this post. Just bear in mind that DSP blocks are useful for many things beyond straight multiplication.
You can also implement multiplication directly in logic (LUTs and flip-flops), but it takes significant resources. Using dedicated DSP blocks for multiplication makes sense from a performance and logic-use perspective. Hence, even small FPGAs dedicate space to DSP blocks.
Multiplication Capabilities
Let’s take a quick look at the multiplication capabilities of a few FPGAs.
The width of a DSP multiplier depends on the FPGA architecture:
- Altera Cyclone V:
27 x 27 bit - Lattice iCE40UP (SB_MAC16):
16 x 16 bit - Lattice ECP5 (sysDSP):
18 x 18 bit - Xilinx 7 Series (DSP48E1):
25 × 18 bit - Xilinx Ultrascale+ (DSP48E2):
27 x 18 bit
For example, an ECP5 multiplier takes two 18-bit inputs and generates a 36-bit product output.
While the number of multipliers depends on the specific FPGA part:
- Altera Cyclone V:
- 5CSEBA6U23I7:
112 multipliers
- 5CSEBA6U23I7:
- Lattice iCE40UP
- iCE40UP5K:
8 multipliers
- iCE40UP5K:
- Lattice ECP5
- LFE5U-85:
156 multipliers - LFE5U-25:
56 multipliers
- LFE5U-85:
- Xilinx 7 Series
- Artix-7 A200T:
740 multipliers - Spartan-7 S25:
80 multipliers
- Artix-7 A200T:
- Xilinx Ultrascale+
- Artix AU10P:
400 multipliers
- Artix AU10P:
Larger FPGAs include many thousands of multipliers, but we’ve confined ourselves to parts you might find on a hobbyist-friendly board (I live in hope of an affordable Ultrascale+ board in 2022 2023).
DSP Block References
- Variable Precision DSP Blocks in Cyclone V Devices
- Lattice DSP Function Usage Guide for iCE40 Devices
- Lattice ECP5 and ECP5-5G sysDSP Usage Guide
- Xilinx 7 Series DSP48E1 Slice
- Xilinx Ultrascale+ DSP48E2 Slice
Note: each ECP5 DSP block incorporates two multipliers and each Cyclone V DSP block can handle one 27x27, two 18x18, or three 9x9 multiplications.
Using DSPs
There are two ways to incorporate DSPs into your FPGA designs:
- Explicitly instantiate the DSP primitive (SB_MAC16, DSP48E1 etc.)
- Infer the DSP using regular multiplication in Verilog or VHDL
Vendor primitives allow you to fine-tune your implementation but are more complex and limit your design to a single FPGA architecture. I’d recommend starting with inference and only reaching for vendor primitives if you need to do something clever or ring the last nanosecond out of your design.
Yosys DSP Inference
If you’re using Yosys with an iCE40UP FPGA, you need to explicitly enable DSP inference using the -dsp option.
For example, to synthesize a module called top_pong.v:
yosys -p "synth_ice40 -dsp -json top_pong.json" top_pong.v
On ECP5, Yosys infers DSPs by default; you can disable them with -nodsp.
Multiplication Examples
To create simple, practical examples, I’ve combined simple maths functions with graphics output. If you have an FPGA board with video output, you can view the results on screen, but even if you don’t, you can still look at the designs and timings with your FPGA development tools. I also provide Verilator simulations of the designs.
Our examples run mathematical functions for each pixel on the screen, generating a 0 or 1 as output. The function needs to keep pace with the display signal: calculating 25 million values per second for 640x480 or 74 million for 1280x720.
Source
The SystemVerilog designs featured in this post are available from the projf-explore git repo under the open-source MIT licence: build on them to your heart’s content. The rest of the blog content is subject to standard copyright restrictions: don’t republish it without permission.
Squared
Let’s start with a module that includes just one multiplication.
This module takes the X and Y coordinates of a pixel and returns 1 if X squared is larger than the scaled Y value (explained below).
module func_squared #(
CORDW=8, // signed coordinate width (bits)
Y_SCALE=256 // increase y-scale so we can see more on-screen
) (
input wire clk,
input wire signed [CORDW-1:0] x,
input wire signed [CORDW-1:0] y,
output logic r
);
// v1: simple version (latency: 2 cycles)
logic signed [2*CORDW-1:0] x_squared;
logic signed [2*CORDW-1:0] y_scaled;
always_ff @(posedge clk) begin
y_scaled <= Y_SCALE * y;
x_squared <= x*x;
r <= (x_squared < y_scaled) ? 1 : 0;
end
endmodule
Because we’re using integers, each pixel represents one whole number. When we square X, the value quickly becomes too large to fit on screen if we assume each vertical pixel represents 1. To make more of the function visible, we scale the Y-axis with a parameter. In this case, we’ve scaled the Y-axis so each pixel represents 256.
Here’s a sample top module to drive it; this version is for the Arty (Xilinx 7 Series). (0,0) is in the centre of the screen. We’re using 12-bit signed signals, so they comfortably fit into any DSP.
module top_graphing (
input wire logic clk_100m, // 100 MHz clock
input wire logic btn_rst, // reset button (active low)
output logic vga_hsync, // horizontal sync
output logic vga_vsync, // vertical sync
output logic [3:0] vga_r, // 4-bit VGA red
output logic [3:0] vga_g, // 4-bit VGA green
output logic [3:0] vga_b // 4-bit VGA blue
);
// generate pixel clock
logic clk_pix;
logic clk_locked;
clock_gen_480p clock_pix_inst (
.clk(clk_100m),
.rst(!btn_rst), // reset button is active low
.clk_pix,
.clk_locked
);
// display sync signals and coordinates
localparam CORDW = 12;
logic hsync, vsync;
logic [CORDW-1:0] sx, sy;
logic de;
display_480p #(.CORDW(CORDW)) display_inst (
.clk_pix,
.rst(!clk_locked),
.sx,
.sy,
.hsync,
.vsync,
.de,
.frame(),
.line()
);
// signal when to draw mathematical function and axis
logic draw, axes;
// VGA output
always_ff @(posedge clk_pix) begin
vga_hsync <= hsync;
vga_vsync <= vsync;
vga_r <= !de ? 4'h0 : (axes ? 4'hC : (draw ? 4'h3 : 4'h2));
vga_g <= !de ? 4'h0 : (axes ? 4'hC : (draw ? 4'hB : 4'h2));
vga_b <= !de ? 4'h0 : (axes ? 4'hC : (draw ? 4'hC : 4'h2));
end
//
// Graphing Logic
//
// function coordinates
logic signed [CORDW-1:0] x, y;
// adjust screen coordinates so (0,0) is at centre of screen
localparam X_OFFS = 320;
localparam Y_OFFS = 239;
always_ff @(posedge clk_pix) begin
x <= sx - X_OFFS + 3; // latency for function (+n) and offset calculation (+1)
y <= Y_OFFS - sy;
end
// draw X and Y axes
logic x_axis, y_axis;
always_comb begin
x_axis = (sy == Y_OFFS);
y_axis = (sx == X_OFFS);
axes = x_axis || y_axis;
end
// function to graph
func_squared #(.CORDW(CORDW)) func_inst (
.clk(clk_pix),
.x,
.y,
.r(draw)
);
endmodule
Building the Demos
In the Maths Demo section of the git repo, you’ll find the design files, a makefile for iCEBreaker, a Vivado project for Arty and Nexys Video, and instructions for building the designs for dev boards and with Verilator.
And here’s what the Verilator simulation looks like:
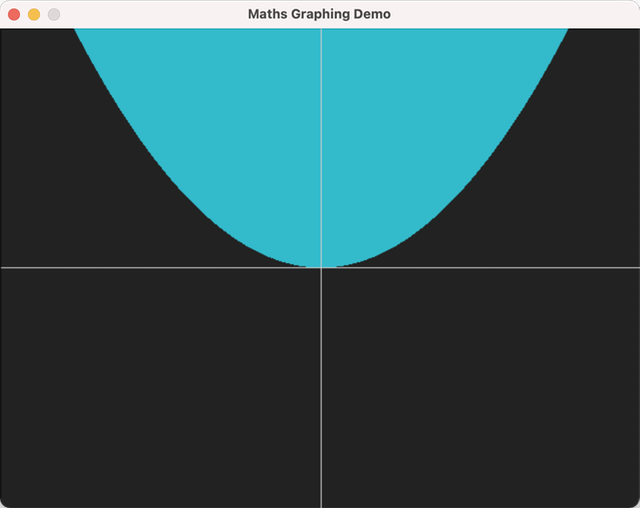
Vivado automatically infers DSPs for the multiplication, but it gives a warning of the form:
[DRC DPOP-2] MREG Output pipelining
Pipelining the multiplier function will improve performance and will save significant power so it is suggested whenever possible to fully pipeline this function. If this multiplier was inferred, it is suggested to describe an additional register stage after this function.
Let’s take Vivado’s advice and register the result of the multiplication before comparing it with the Y-value. This adds an additional cycle of latency, so we need to delay the Y value:
// v2: extra pipeline stages (latency: 3 cycles)
logic signed [2*CORDW-1:0] x_squared, x_squared_p1;
logic signed [2*CORDW-1:0] y_scaled, y_scaled_p1;
always_ff @(posedge clk) begin
y_scaled_p1 <= Y_SCALE * y;
y_scaled <= y_scaled_p1;
x_squared_p1 <= x*x;
x_squared <= x_squared_p1;
r <= (x_squared < y_scaled) ? 1 : 0;
end
We also update the latency correction in top_graphing; otherwise our results don’t match our inputs and our graphic would be shifted to the right:
x <= sx - X_OFFS + 4; // latency for function (+n) and offset calculation (+1)
Let’s compare the timings and logic used for the two versions of the design on different FPGAs:
| FPGA | Design | Target | Cycles | LUT | FF | DSP | WNS (ns) |
|---|---|---|---|---|---|---|---|
| XC7A35T | Squared v1 | 25.2 MHz | 2 | 81 | 90 | 1 | 33.6 |
| XC7A35T | Squared v2 | 25.2 MHz | 3 | 84 | 96 | 1 | 34.1 |
| XC7A200T | Squared v1 | 74.25 MHz | 2 | 137 | 127 | 1 | 9.2 |
| XC7A200T | Squared v2 | 74.25 MHz | 3 | 139 | 135 | 1 | 8.2 |
Built with Vivado 2021.2 using default settings for synthesis and implementation. Xilinx FPGAs are speed grade -1 (slowest grade).
The results for XC7A35T include 640x480 VGA output, while those for XC7A200T include 1280x720p60 DVI output. Timing (represented by WNS) wasn’t an issue for 25 or 74 MHz operation, even with the first version of our design. The extra pipeline stage uses a little more logic and adds an additional cycle of latency.
Timing on the XC7A200T is actually worse for our pipelined design, but still comfortable. Vivado doesn’t optimise a design when timing is comfortable, so we shouldn’t read too much into this.
Worst Negative Slack
The unhelpfully named worst negative slack (WNS) is how Vivado reports timing. The larger this number, the better, but you need to account for the target clock speed. For example, at 100 MHz the maximum WNS is 10 ns because that’s how long a clock cycle lasts at 100 MHz. If WNS is negative, your design doesn’t meet timing and might not work.
Circle
A more complex function is the circle equation, which requires squaring both X and Y.
Again, we create two versions and compare them. I’m including both versions in one module but commented one out.
module func_circle #(
CORDW=8, // signed coordinate width (bits)
RADIUS=128 // circle radius
) (
input wire clk,
input wire signed [CORDW-1:0] x,
input wire signed [CORDW-1:0] y,
output logic r
);
// // v1: simple version (latency: 2 cycles)
// logic signed [2*CORDW:0] circle; // addition of two squares, so twice as wide
// always_ff @(posedge clk) begin
// circle <= x*x + y*y;
// r <= (circle < RADIUS * RADIUS) ? 1 : 0;
// end
// v2: extra pipeline stages (latency: 4 cycles)
logic [2*CORDW-1:0] x_squared, x_squared_p1;
logic [2*CORDW-1:0] y_squared, y_squared_p1;
logic signed [2*CORDW:0] circle; // addition of two squares, so twice as wide
always_ff @(posedge clk) begin
x_squared_p1 <= x*x;
x_squared <= x_squared_p1;
y_squared_p1 <= y*y;
y_squared <= y_squared_p1;
circle <= x_squared + y_squared;
r <= (circle < RADIUS * RADIUS) ? 1 : 0;
end
endmodule
| FPGA | Design | Target | Cycles | LUT | FF | DSP | WNS (ns) |
|---|---|---|---|---|---|---|---|
| XC7A35T | Circle v1 | 25.2 MHz | 2 | 78 | 66 | 2 | 33.6 |
| XC7A35T | Circle v2 | 25.2 MHz | 4 | 102 | 77 | 2 | 33.9 |
| XC7A200T | Circle v1 | 74.25 MHz | 2 | 135 | 103 | 2 | 7.7 |
| XC7A200T | Circle v2 | 74.25 MHz | 4 | 159 | 114 | 2 | 9.2 |
As with our squared module, we’ve so much timing slack at 25 MHz that the extra registers don’t make any significant difference. At 74 MHz there is some improvement, but both versions have generous slack considering the target frequency.
NB. This is not an efficient way to draw a circle for graphics applications; use a specialist circle drawing algorithm that doesn’t require DSPs, such as the one in FPGA Shapes.
Cubed
The next example increases the complexity a little more, calculating X cubed:
module func_cubed #(
CORDW=8, // signed coordinate width (bits)
Y_SCALE=16384 // increase y-scale so we can see more on-screen
) (
input wire clk,
input wire signed [CORDW-1:0] x,
input wire signed [CORDW-1:0] y,
output logic r
);
// // v1: simple version (latency: 2 cycles)
// logic signed [3*CORDW-1:0] x_cubed, y_scaled;
// always_ff @(posedge clk) begin
// y_scaled <= Y_SCALE * y;
// x_cubed <= x*x*x;
// r <= (x_cubed < y_scaled) ? 1 : 0;
// end
// v2: extra pipeline stages (latency: 5 cycles)
logic signed [2*CORDW-1:0] x_squared, x_squared_p1;
logic signed [3*CORDW-1:0] x_cubed_p1, x_cubed;
logic signed [3*CORDW-1:0] y_scaled, y_scaled_p1, y_scaled_p2, y_scaled_p3;
always_ff @(posedge clk) begin
y_scaled_p3 <= Y_SCALE * y;
y_scaled_p2 <= y_scaled_p3;
y_scaled_p1 <= y_scaled_p2;
y_scaled <= y_scaled_p1;
x_squared_p1 <= x*x;
x_squared <= x_squared_p1;
x_cubed_p1 <= x*x_squared;
x_cubed <= x_cubed_p1;
r <= (x_cubed < y_scaled) ? 1 : 0;
end
endmodule
In the initial version of cubed, we have two multiplications in one expression. Interestingly, if the signal width is 16, it requires three DSPs, while 12-bit signals need only two. This is another reason to infer DSPs for multiplication: synthesis tools can make non-obvious optimisations.
Adding the extra pipeline stages and registers makes a more noticeable difference:
| FPGA | Design | Target | Cycles | LUT | FF | DSP | WNS (ns) |
|---|---|---|---|---|---|---|---|
| XC7A35T | Cubed v1 | 25.2 MHz | 2 | 83 | 90 | 2 | 30.7 |
| XC7A35T | Cubed v2 | 25.2 MHz | 5 | 91 | 79 | 3 | 33.9 |
| XC7A200T | Cubed v1 | 74.25 MHz | 2 | 140 | 127 | 2 | 4.6 |
| XC7A200T | Cubed v2 | 74.25 MHz | 5 | 148 | 115 | 3 | 9.1 |
For our 25 MHz design, we’ve still got plenty of slack, but the additional pipeline stages improve performance at the cost of an extra DSP. However, the number of flip flops goes down in the pipelined version. The 74 MHz results mirror 25 MHz, though timing is starting to get tight for the non-pipelined design.
Quartic Polynomial
Let’s up the ante and graph a quartic polynomial: x⁴−x².
module func_polynomial #(
CORDW=8, // signed coordinate width (bits)
Y_SCALE=2**24 // increase y-scale so we can see more on-screen
) (
input wire clk,
input wire signed [CORDW-1:0] x,
input wire signed [CORDW-1:0] y,
output logic r
);
// // v1: simple version (latency: 2 cycles)
// logic signed [4*CORDW-1:0] x_poly, y_scaled;
// always_ff @(posedge clk) begin
// y_scaled <= Y_SCALE * y;
// x_poly <= x*x*x*x - 2**16 * x*x;
// r <= (x_poly < y_scaled) ? 1 : 0;
// end
// v2: extra pipeline stages (latency: 6 cycles)
logic signed [2*CORDW-1:0] x_squared, x_squared_p1, x_squared_p2, x_squared_p3;
logic signed [4*CORDW-1:0] x_fourth, x_fourth_p1, x_poly;
logic signed [4*CORDW-1:0] y_scaled, y_scaled_p1, y_scaled_p2, y_scaled_p3, y_scaled_p4;
always_ff @(posedge clk) begin
y_scaled_p4 <= Y_SCALE * y;
y_scaled_p3 <= y_scaled_p4;
y_scaled_p2 <= y_scaled_p3;
y_scaled_p1 <= y_scaled_p2;
y_scaled <= y_scaled_p1;
x_squared_p3 <= x*x;
x_squared_p2 <= x_squared_p3;
x_squared_p1 <= x_squared_p2;
x_squared <= x_squared_p1;
x_fourth_p1 <= x_squared_p2 * x_squared_p2;
x_fourth <= x_fourth_p1;
x_poly <= x_fourth - 2**16 * x_squared;
r <= (x_poly < y_scaled) ? 1 : 0;
end
endmodule
| FPGA | Design | Target | Cycles | LUT | FF | DSP | WNS (ns) |
|---|---|---|---|---|---|---|---|
| XC7A35T | Polynomial v1 | 25.2 MHz | 2 | 130 | 112 | 6 | 20.9 |
| XC7A35T | Polynomial v2 | 25.2 MHz | 6 | 150 | 160 | 3 | 33.1 |
| XC7A200T | Polynomial v1 | 74.25 MHz | 2 | 186 | 149 | 6 | - 2.7 |
| XC7A200T | Polynomial v2 | 74.25 MHz | 6 | 206 | 198 | 3 | 7.6 |
This time there’s a significant difference in timing, even at 25 MHz. For 74 MHz, the complexity has caught up with us, and v1 misses timing by quite a margin. However, the pipelined version is still comfortable.
Notably, the extra pipeline stages also halve the number of DSPs required from 6 to 3. Don’t assume that adding pipeline stages results in higher DSP usage: handling too much complex logic in one cycle can be inefficient in logic as well as time.
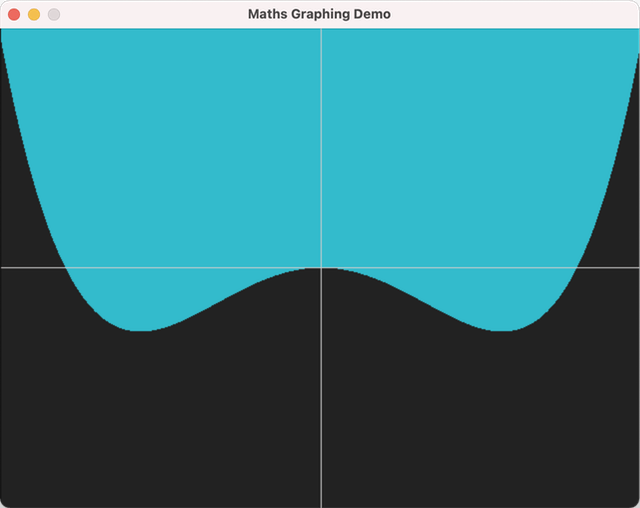
A Balancing Act
Implementing an algorithm in hardware is always a balancing act, never more so than when using DSPs. Adding pipeline stages and registering outputs is almost always worthwhile, but it does increase latency, which is problematic for some applications. Using narrower signals saves logic but reduces accuracy or range.
I’ll finish by giving you a few tips to take away:
- Improve timing by including at least one register between each calculation step
- Narrower signals can save significant DSPs and logic
- Use signed values with Xilinx DSPs
- Use an FSM to divide a complex algorithm into multiple steps
- We’ll see examples of using FSM with algorithms in later posts
Next Time
In our fourth installment we get an introduction to Fixed-Point Numbers in Verilog or try rendering the Mandelbrot Set in Verilog.