Life on Screen
In this FPGA demo we’ll experiment with Game of Life, a cellular automaton created by prolific mathematician John Conway in 1970.
NB. This demo uses an old framebuffer design. For new projects, I recommend following Framebuffers.
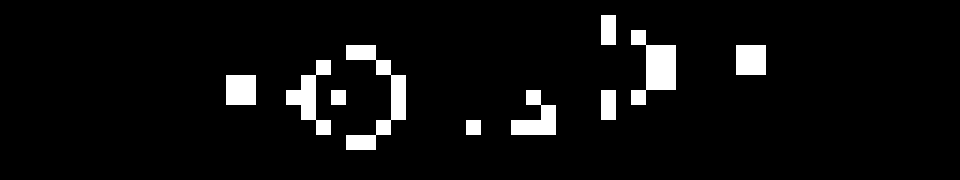
Requirements
For this demo you need an FPGA board with video output. I’ll be working with the Digilent A7 Arty, but it should be easy to adapt this design to other boards. It helps to be comfortable with programming your FPGA board and reasonably familiar with Verilog.
If you’ve not played with FPGA graphics before, check out Beginning FPGA Graphics.
Conway’s Life
He is Archimedes, Mick Jagger, Salvador Dalí, and Richard Feynman, all rolled into one.
The Guardian, John Horton Conway: the world’s most charismatic mathematician (2015)
John Conway was a remarkable mathematician, active in many fields, who sadly died in 2020. Conway is best known to the public for recreational mathematics with Martin Gardner in Scientific American. I remember playing Sprouts at school and trying to impress people by calculating the day of the week with the Doomsday rule. For now, I’ll be limiting myself to Game of Life, but I highly recommend learning more of Conway: The world’s most charismatic mathematician is an excellent place to start.
Game of Life first appeared in the Mathematical Games column in the October 1970 issue of Scientific American. Anyone can access the article at ibiblio.org, or you can see a scan of the original at JSTOR (requires login via academic institution or library).
The Rules of Life
The universe of the Game of Life is an infinite, two-dimensional, grid of cells. A cell is one of two states: dead or alive. Every cell interacts with its eight neighbours (those to the left, right, top, bottom, and the four diagonals).
The following rules determine the fate of a cell in the next generation:
- Survival: Every cell with two or three neighbours survives.
- Deaths:
a. Every cell with four or more neighbours dies from overpopulation.
b. Every cell with zero or one neighbours dies from isolation. - Births: Every empty cell with exactly three neighbours comes to life.
To understand this, it helps to see some practical examples. Common patterns within the Life universe have been given names. The diagram below shows two patterns: “Beehive” and “Beacon”.

Every live cell in the Beehive pattern has two or three neighbours: so, no cells die. No dead cells in Beehive have three neighbours: so, no cells come to life. This pattern is categorised as a “still life”, because it doesn’t change from one generation to the next.
The Beacon pattern is a bit more interesting: it oscillates between two states. Two dead cells in the centre of the pattern have three neighbours, so come to life. However, they then have four neighbours, so die the next generation due to overcrowding: this pattern repeats endlessly.
However, things start to get really interesting with slightly more complex patters. The following photo shows the Gosper glider gun running on the Arty board. The gun repeatedly generates small patterns called gliders that step across the world.

It’s even possible to construct logic gates using gliders, and ultimately a universal Turing machine. For this little demo, we’re not going to dig further into the esoteric possibilities of Conway’s Life, but check out Wikipedia’s article on Conway’s Game of Life.
A Hard Life
Now we have a basic understanding of Life, we’re going to create a hardware implementation.
Let’s start by rearranging the rules to simplify the design:
- If a cell is alive
a. if it has 2 or 3 neighbours, it’s alive next generation
b. otherwise, it’s dead next generation - If a cell is dead
a. if it has 3 neighbours, it’s alive next generation
b. otherwise, it’s dead next generation
We need a two-dimensional array to hold our world. Our memory array obviously can’t be infinite, so we need a way to handle the edges.
- Surround the world with a border of dead cells
- Wrap the world around at left and right, and at top and bottom
Both approaches have their advantages and disadvantages, but I’ll be using option 1 for this demo.
Since a cell’s state depends on all those around it, we can’t calculate the new state of each cell with one array. Instead, we have two array (or buffers): one contains the current generation; we use it to calculate the next generation in the second buffer. Every generation, we swap buffers and repeat the generation process.
Life Module
The rules of life are expressed in [life.sv]:
module life #(
parameter CORDW=16, // signed coordinate width
parameter WIDTH=6, // world width in cells
parameter HEIGHT=6, // world height in cells
parameter F_INIT="" // initial world state
) (
input wire logic clk, // clock
input wire logic rst, // reset
input wire logic start, // start generation
output logic ready, // cell state ready to be read
output logic alive, // is the cell alive? (when ready)
output logic changed, // cell's state changed (when ready)
output logic signed [CORDW-1:0] x, // horizontal cell position
output logic signed [CORDW-1:0] y, // vertical cell position
output logic running, // life is running
output logic done // generation complete (high for one tick)
);
// world buffer selection
logic next_gen; // where to write the next generation
always_ff @(posedge clk) begin
if (start) next_gen <= ~next_gen; // swap every generation
if (rst) next_gen <= 0;
end
// world in BRAM
localparam DATAW = 1; // cells are either dead or alive
localparam WORLD_WIDTH = WIDTH + 2; // wider to handle boundary
localparam WORLD_HEIGHT = HEIGHT + 2; // taller to handle boundary
localparam WORLD_CELLS = WORLD_WIDTH * WORLD_HEIGHT;
localparam DEPTH = 2 * WORLD_CELLS;
localparam ADDRW = $clog2(DEPTH);
logic we;
logic [ADDRW-1:0] cell_id, addr_read; // cell_id is basis of write address
logic [DATAW-1:0] data_in, data_out;
// add offset to read and write addresses to match buffer used
logic [ADDRW-1:0] addr_read_offs, addr_write_offs;
always_comb begin
addr_read_offs = addr_read + ((next_gen) ? 0 : WORLD_CELLS);
addr_write_offs = cell_id + ((next_gen) ? WORLD_CELLS : 0);
end
bram_sdp #(
.WIDTH(DATAW),
.DEPTH(DEPTH),
.INIT_F(F_INIT)
) bram_inst (
.clk_write(clk),
.clk_read(clk),
.we,
.addr_write(addr_write_offs),
.addr_read(addr_read_offs),
.data_in,
.data_out
);
// cell coordinates
localparam GRID = 3; // neighbours are a 3x3 grid
localparam STEPS = 11; // 9 reads and 2 cycles of latency
logic [$clog2(WORLD_WIDTH)-1:0] cell_x; // active cell (horizontal)
logic [$clog2(WORLD_HEIGHT)-1:0] cell_y; // active cell (vertical)
logic [$clog2(STEPS)-1:0] read_step; // reading step
logic inc_read; // perform incremental read
logic [GRID-1:0] top_sr, mid_sr, bot_sr; // shift reg for neighbours
logic [$clog2(GRID*GRID)-1:0] neigh_cnt; // count of neighbours
// life generation state
enum {IDLE, INIT, READ, NEIGH, UPDATE, NEW_CELL, NEW_LINE} state;
always_ff @(posedge clk) begin
// single-cycle flags: 0 by default
ready <= 0;
we <= 0;
done <= 0;
case(state)
INIT: begin
read_step <= 0;
inc_read <= 0;
top_sr <= 0;
mid_sr <= 0;
bot_sr <= 0;
neigh_cnt <= 0;
state <= READ;
running <= 1;
// first cell after padding
cell_x <= 1;
cell_y <= 1;
cell_id <= WORLD_WIDTH + 1;
end
READ: begin // 1 cycle to set address and 1 cycle BRAM read latency
case (read_step)
4'd0: begin
addr_read <= cell_id - WORLD_WIDTH - 1; // A
end
4'd1: begin
addr_read <= cell_id - 1; // B
end
4'd2: begin
addr_read <= cell_id + WORLD_WIDTH - 1; // C
if (!inc_read) top_sr <= {top_sr[1:0], data_out}; // A
end
4'd3: begin
addr_read <= cell_id - WORLD_WIDTH; // D
if (!inc_read) mid_sr <= {mid_sr[1:0], data_out}; // B
end
4'd4: begin
addr_read <= cell_id; // E
if (!inc_read) bot_sr <= {bot_sr[1:0], data_out}; // C
end
4'd5: begin
addr_read <= cell_id + WORLD_WIDTH; // F
if (!inc_read) top_sr <= {top_sr[1:0], data_out}; // D
end
4'd6: begin
addr_read <= cell_id - WORLD_WIDTH + 1; // G
if (!inc_read) mid_sr <= {mid_sr[1:0], data_out}; // E
end
4'd7: begin
addr_read <= cell_id + 1; // H
if (!inc_read) bot_sr <= {bot_sr[1:0], data_out}; // F
end
4'd8: begin
addr_read <= cell_id + WORLD_WIDTH + 1; // I
top_sr <= {top_sr[1:0], data_out}; // G
end
4'd9: begin
mid_sr <= {mid_sr[1:0], data_out}; // H
end
4'd10: begin
bot_sr <= {bot_sr[1:0], data_out}; // I
end
default: addr_read <= 0;
endcase
if (read_step == STEPS-1) state <= NEIGH;
else read_step <= read_step + 1;
end
NEIGH: begin
neigh_cnt <= top_sr[0] + top_sr[1] + top_sr[2] +
mid_sr[0] + mid_sr[2] +
bot_sr[0] + bot_sr[1] + bot_sr[2];
state <= UPDATE;
end
UPDATE: begin
// update cell state
we <= 1; // write new cell state next cycle
ready <= 1; // ready for output next cycle
x <= cell_x - 1; // correct horizontal position for padding
y <= cell_y - 1; // correct vertical position for padding
if (mid_sr[1]) begin // cell was alive this generation
if (neigh_cnt == 2 || neigh_cnt == 3) begin // still alive
data_in <= 1;
alive <= 1;
changed <= 0;
end else begin // now dead
data_in <= 0;
alive <= 0;
changed <= 1;
end
end else begin // was dead this generation
if (neigh_cnt == 3) begin // now alive
data_in <= 1;
alive <= 1;
changed <= 1;
end else begin // still dead
data_in <= 0;
alive <= 0;
changed <= 0;
end
end
// what next?
if (cell_x == WORLD_WIDTH-2) begin // final cell on line
if (cell_y == WORLD_HEIGHT-2) begin // final line of cells
state <= IDLE;
running <= 0;
done <= 1;
end else state <= NEW_LINE;
end else state <= NEW_CELL;
end
NEW_CELL: begin
cell_x <= cell_x + 1;
cell_id <= cell_id + 1;
inc_read <= 1; // incremental read
read_step <= 6; // read new column of 3 cells (skip A-F)
state <= READ;
end
NEW_LINE: begin
cell_y <= cell_y + 1;
cell_x <= 1;
cell_id <= cell_id + 3; // skip 2 cells of padding
read_step <= 0; // read all nine cells at start of line
state <= READ;
end
default: state <= (start) ? INIT : IDLE; // IDLE
endcase
if (rst) begin
state <= IDLE;
ready <= 0;
alive <= 0;
changed <= 0;
x <= 0;
y <= 0;
running <= 0;
done <= 0;
end
end
endmodule
To exercise this module I’ve created test bench for Vivado: [life_tb.sv].
Top Life
I’ve created a top module for the Arty board to run the life instance - [xc7/top_life.sv]:
module top_life (
input wire logic clk_100m, // 100 MHz clock
input wire logic btn_rst_n, // reset button (active low)
output logic vga_hsync, // horizontal sync
output logic vga_vsync, // vertical sync
output logic [3:0] vga_r, // 4-bit VGA red
output logic [3:0] vga_g, // 4-bit VGA green
output logic [3:0] vga_b // 4-bit VGA blue
);
localparam GEN_FRAMES = 15; // each generation lasts this many frames
localparam SEED_FILE = "simple_64x48.mem"; // world seed
// localparam SEED_FILE = "gosper_gun_64x48.mem"; // world seed
// generate pixel clock
logic clk_pix;
logic clk_pix_locked;
logic rst_pix;
clock_480p clock_pix_inst (
.clk_100m,
.rst(!btn_rst_n), // reset button is active low
.clk_pix,
.clk_pix_5x(), // not used for VGA output
.clk_pix_locked
);
always_ff @(posedge clk_pix) rst_pix <= !clk_pix_locked; // wait for clock lock
// display sync signals and coordinates
localparam CORDW = 16;
logic hsync, vsync;
logic de, frame, line;
display_480p #(.CORDW(CORDW)) display_inst (
.clk_pix,
.rst_pix,
.sx(),
.sy(),
.hsync,
.vsync,
.de,
.frame,
.line
);
logic frame_sys; // start of new frame in system clock domain
xd xd_frame (.clk_src(clk_pix), .clk_dst(clk_100m),
.flag_src(frame), .flag_dst(frame_sys));
// life signals
logic life_start, life_alive, life_changed;
// start life generation in blanking every GEN_FRAMES
logic [$clog2(GEN_FRAMES)-1:0] cnt_frames;
always_ff @(posedge clk_100m) begin
life_start <= 0;
if (frame_sys) begin
if (cnt_frames == GEN_FRAMES-1) begin
life_start <= 1;
cnt_frames <= 0;
end else cnt_frames <= cnt_frames + 1;
end
end
// framebuffer (FB)
localparam FB_WIDTH = 64;
localparam FB_HEIGHT = 48;
localparam FB_CIDXW = 2;
localparam FB_CHANW = 4;
localparam FB_SCALE = 10;
localparam FB_IMAGE = "";
localparam FB_PALETTE = "life_palette.mem";
logic fb_we;
logic signed [CORDW-1:0] fbx, fby; // framebuffer coordinates
logic [FB_CIDXW-1:0] fb_cidx;
logic fb_busy; // when framebuffer is busy it cannot accept writes
logic [FB_CHANW-1:0] fb_red, fb_green, fb_blue; // colours for display
framebuffer_bram #(
.WIDTH(FB_WIDTH),
.HEIGHT(FB_HEIGHT),
.CIDXW(FB_CIDXW),
.CHANW(FB_CHANW),
.SCALE(FB_SCALE),
.F_IMAGE(FB_IMAGE),
.F_PALETTE(FB_PALETTE)
) fb_inst (
.clk_sys(clk_100m),
.clk_pix,
.rst_sys(1'b0),
.rst_pix(1'b0),
.de,
.frame,
.line,
.we(fb_we),
.x(fbx),
.y(fby),
.cidx(fb_cidx),
.busy(fb_busy),
.clip(),
.red(fb_red),
.green(fb_green),
.blue(fb_blue)
);
// select colour based on cell state
always_comb fb_cidx = {1'b0, life_alive};
life #(
.CORDW(CORDW),
.WIDTH(FB_WIDTH),
.HEIGHT(FB_HEIGHT),
.F_INIT(SEED_FILE)
) life_inst (
.clk(clk_100m), // clock
.rst(1'b0), // reset
.start(life_start), // start generation
.ready(fb_we), // cell state ready to be read
.alive(life_alive), // is the cell alive? (when ready)
.changed(life_changed), // cell's state changed (when ready)
.x(fbx), // horizontal cell position
.y(fby), // vertical cell position
.running(), // life is running
.done() // generation complete (high for one tick)
);
// reading from FB takes one cycle: delay display signals to match
logic hsync_p1, vsync_p1;
always_ff @(posedge clk_pix) begin
hsync_p1 <= hsync;
vsync_p1 <= vsync;
end
// VGA output
always_ff @(posedge clk_pix) begin
vga_hsync <= hsync_p1;
vga_vsync <= vsync_p1;
vga_r <= fb_red;
vga_g <= fb_green;
vga_b <= fb_blue;
end
endmodule
I’ve used a 64x48 world, which is a tenth of the 640x480 screen dimensions. With the padding of dead cells, each world array has 66 x 50 = 3,300 cells, which comfortably fits into 4Kb.
Building the Demo
In the Life on Screen section of the git repo, you’ll find the design files and build instructions.
Once you’ve programmed your board, you should see a simple test pattern of oscillators and a still life (capture from FPGA board shown below).
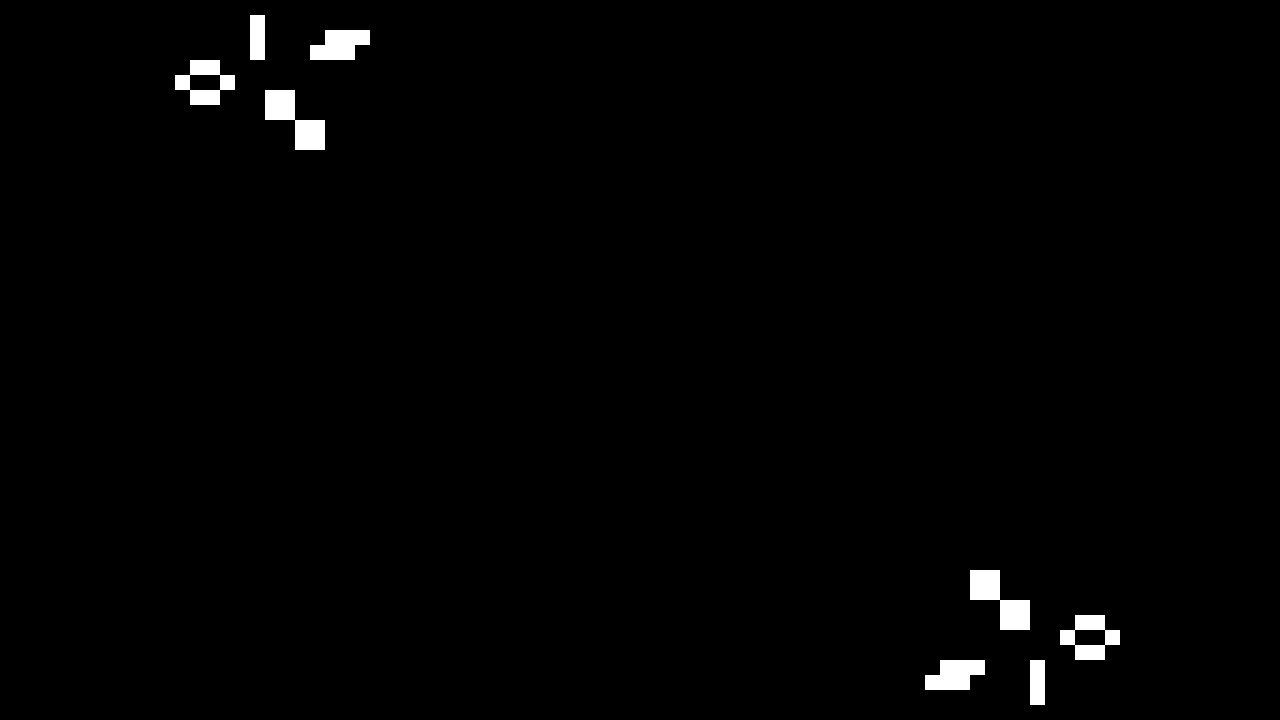
If that works, try the Gosper glider gun by changing the seed file in top_life.sv:
localparam SEED_FILE = "gosper_gun_64x48.mem"; // world seed
The Gosper pattern repeatedly generates small gliders that move down the screen. Our gliders doesn’t continue indefinitely because our world is currently surrounded by dead cells, which kill the gliders when they collide with it.
You can also change how fast Life runs by adjusting GEN_FRAMES:
localparam GEN_FRAMES = 4; // each generation lasts this many frames
At 60 frames per second, a value of ‘4’ results in 15 generations per second.
What’s Next?
Check out my FPGA graphics tutorials.
Peter Hizalev has written a version of Game of Life in Chisel that simulates every cell simultaneously!